An Interrelated Earth-Moon System

The spin-orbits of the Earth and Moon inherently divide the time stream into a functional arrangement
Interfacing lunisolar cycles
It's very easy to recognize that the spin and orbital movements directly divide the time stream into equally metered divisions. For example, the Earth rotates once every 24 hours, the Moon passes through one synodic revolution every 29.53059 days (on the average), and the Earth passes through one Tropical Year every 365.24219 days. Of significance here is that a careful study of these cycles can come to see that the spin-orbits appear to progress in-pace with a time grid that is intelligently arranged.
A functional Moon
Let's begin by exploring the phase rate of the Moon. Take note here that each synodic revolution of the Moon passes through four distinct quarter phases--as follows:
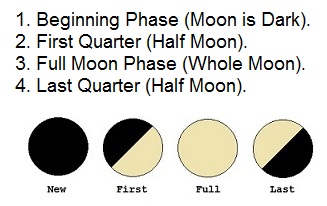
For the purposes of presenting a clear analysis, the quarter-phase cycle of the Moon will hereafer be refered to as the lunar-week cycle. Likewise, the time span of any specific quarter phase of the Moon will hereafter be refered to as the span of a lunar week. Note that each lunar week averages out to be about equal to seven and one-third days. The cycle of the lunar week is consequently a bit slower or longer than an ordinary week cycle of 7 days.
A time grid of lunar weeks can be shown to almost exactly overlay a time grid of solar years. In essence, based upon the spin and orbital phenomenon, the rate of the lunar-week cycle is easy to illustrate in cross-reference with the rate of the tropical year.
The inherent lunisolar overlay is based upon the modern rate of the lunar-quarter phase. It is here significant that ancient eclipse data indicates that the spin and orbital rates tend to vary by a tiny amount throughout time. Consequently, a time grid of lunar quarters may have once existed in perfect interface with a time grid of solar years. For additional information concerning the long-term accuracy and definition of the cited interface, refer to the following online document--
What is remarkable here is that the track of a cycle of 7 sets of 7 years (plus a 50th year) can be recited from ancient Israelite literature (including biblical). Some texts produced in the Second-Temple Era explicitly describe the rotation of the priestly courses in association with a jubilee schedule. When detailing the priestly rotation in association with a 49-year cycle, Scroll 4QOtot becomes rather explicit in describing the appearance of a lunar-cycle 'sign' (the 'ot', or plural 'otot') at the unending frequency of each third year. The source information that relates the early adherence to 7 sets of 7 years (and associated lunar-cycle reckoning) seems to mirror the possibility that Israel's priesthood possessed knowledge of the above cited jubilee interface. For additional information concerning the once adhered to count of 50 years, refer to the online publication:
More about the Moon
The previously presented section has attempted to show that the Moon cycle does seem to intelligently interrelate both with the annual transit of the Sun (the solar-year rate) and also with the spin of the Earth (the solar-day rate).
A degree of interrelated time design can additionally be interpreted from the peculiar rate by which the synodic month of 29.53059 days does exceed a whole day rate of 29 days.
Take note that an amount of difference is inherent between the rate of the synodic month (29.53059 days on the average) and a whole-day count of 29 days. The cited difference between the two rates averages out to be a little over half a day--or 0.53059 days. (Note that 29.53059 days minus 29 days is equal to 0.53059 days).
Based upon the indicated half-day count difference by which the synodic month exceeds 29 days, it follows that if the rate of the synodic month is always counted out in correspondence with a whole-day rate (29 days) then the difference of the stated half-day rate (0.53059 days per lunar month) would eventually accumulate or accrue to the sum of exactly 105 days in every cycle of 16 solar years.
The indicated correspondence between cycles of the Earth, Moon, and Sun seems significant in the regard that 105 days in 16 years is all but perfectly equal to the rate of 0.53059 days per lunar month.
Thus, the rate of the lunar-month in excess of 29 days (or 105 days in 16 tropical years) can be recognized to come astride the passage of 16 solar years to within an average match of only 30 seconds. (This is a difference of less than 2 seconds per year!)
The cited rate of 105 days can then almost perfectly be scribed relative to the rate of 16 tropical years; however, because the spin of the Earth appears to be slowing with time then this respective solar-day count can be predicted to have been absolutely perfect in the relatively recent past. For more information, refer to the following online publication:
Note that if the period of the Moon cycled at a rate exactly equal to 29.5 days per synodic month then a 30th day could simply be intercalated every alternate month. However, the actual synodic revolution in 29.53059 days is 44 minutes and 3 seconds slower than 29.50000 days. This respective difference--if prorated on a straight-line basis--would mandate that an additional day always be intercalated every 55.65614 days (on the average). [Note that each tropical year inherently contains 12.368267 lunar months. This number of months when multiplied by an excess over 29 days of 0.53059 days per month is equal to 6.56248 additional days per tropical year--on the average. (This rate is also equal to 1 additional day every 55.65614 days . . . or is equal to 104.99965 additional days every 16 tropical years).]
Time stations
An ancient astronomer left record of the year becoming "complete according to the station of the Moon, and the station of the Sun... ". This notation of 'time stations' seems significant in the regard that the length of each passing solar year can very effectively (almost perfectly) be measured and metered by simply counting solar days. In essence, the length of the solar year (365.24219 days) can almost EXACTLY be correlated to a fixed number of annual days. (This axiom is valid in the context of additionally counting days positioned eternally at Sun and Moon stations).
To be more specific about the definition of time stations, a day count of the tropical year is possible within the context of tracking only the following two time cycles:
- A cycle defined by the Moon.
- A cycle defined by the Sun.
The first of the two cited time cycles that must always be accounted for is equal to 7 lunar weeks. The revolution of a time span equal to 7 lunar weeks must eternally be time tracked--as follows:
------------------------------------ Moon Cycle of 7 Lunar Weeks ------------------------------------ Lunar quarter 1 (lunar week) Lunar quarter 2 (lunar week) Lunar quarter 3 (lunar week) Lunar quarter 4 (lunar week) Lunar quarter 5 (lunar week) Lunar quarter 6 (lunar week) Lunar quarter 7 (lunar week) ------------------------------------
The second of the two time cycles that must always be tracked is equal to the span of time occupied by 30 solar days. The revolution of a time span equal to 30 solar days must eternally be time tracked--as follows: 30 days . . . 30 days . . . 30 days . . . over and over and over.
Of significance here is that one of the best possible day-count models that can account for each passing tropical year requires only a running count of the two stated cycles (7 quarters by the Moon, and 30 days by the Sun).
Please take note here that an intercalation rate equal to 1 day per Sun Cycle and 1 day per Moon Cycle is equal to 19.24232 days per year. This then means that from year to year the seasonal turns can effectively be metered out in correspondence with a fixed count of days. Note that a calendar count of 346 days with intercalated days achieves an average solar-year rate of 365.24232 days.
Thus the average result of tracking days within the context of Sun and Moon cycles (in this modern era) is proven to be perfect from year-to-year within a difference of only 11 seconds! (The annual result of tracking celestial time stations can be recognized as fully or absolutely perfect only centuries before).
Refer to the following online publications for more complete information concerning the significance of tracking celestial time stations:
Functional Time Design A Circle of Sevens The Lunar Week
Day and year cycles
Another characteristic of interrelated time design is the rate by which Earth's spin interfaces with the annual transit of the Sun. Of significance here is that when the solar-day rate is continuosly accounted for in 40-day loops then the length of each solar year can exactly be determined.
To be more specific, each passing solar year can very effectively (even perfectly!) be metered by keeping track of every 40th day. Essentially, the annual transit which completes every 365.24219 days can just about EXACTLY be measured (on the average) via a simple method of scribing each 40th day!
This respective axiom is easy to prove in the regard that the rate of 1 day in a cycle of 40 days (the 40th day) inherently comprises 2.5 percent of the time stream. This rate is also inherently equal to 9.131055 days per year (on average).
For more complete information concerning a time track of 40 days, refer to these online publications:
Significance of 40 Days A Count of 360 Days Ancient Astronomy
A functional time tracking system
In summary to the above, it is significant that the solar day (of 24 hours), the synodic moon (of 29.53059 days, and Earth's annual transit (in 365.24219 days) can be recognized within the context of a system that is functional in its design.
It is then an essential system view that can recognize Divine planning and purpose throughout the solar system. Clearly, the spin and orbital configuration of the Earth, Moon, and Sun has to represent more than mindless design.
________________________________________
Please feel free to download and distribute--but not sell--the articles and booklets listed above. (Note that the published material is subject to constant revision. Be advised that corrections, amendments, and new interpretations are frequently made.)
Copyright © 2002-2026
A-Quest-for-Creation-Answers